Water Vapor Pressure Formulations

Holger Vömel
National Center for Atmospheric Research
Earth Observing Laboratory
Boulder, CO
 

A large number of saturation vapor pressure equations exist to calculate the pressure of water vapor over a surface of liquid water or ice. This is a brief overview of the most important equations used. Several useful reviews of the existing vapor pressure curves are listed in the references.

 

Sections on this page:

  1. Vapor Pressure over liquid water below 0°C
  2. Vapor Pressure over ice
  3. References

 

1. Vapor pressure over liquid water below 0°C

1: Goff Gratch equation
Smithsonian Tables, 1984, after Goff and Gratch, 1946		 Log10 ew =  -7.90298 (373.16/T-1)
                    + 5.02808 Log10(373.16/T) 
                    - 1.3816 10-7 (1011.344 (1-T/373.16)  -1) 
                    + 8.1328 10-3 (10-3.49149 (373.16/T-1)  -1) 
                    + Log10(1013.246) 
with T in [K] and ew in [hPa]
2: Guide to Meteorological Instruments and Methods of Observation (CIMO Guide)
WMO, 2008		 ew = 6.112 e(17.62 t/(243.12 + t)) 
with t in [°C] and ew in [hPa]
3: WMO
Goff, 1957; WMO, 2012		 Log10 ew =  10.79574 (1-273.16/T)
                    - 5.02800 Log10(T/273.16) 
                    + 1.50475 10-4 (1 - 10(-8.2969*(T/273.16-1))) 
                    + 0.42873 10-3 (10(+4.76955*(1-273.16/T)) - 1) 
                    + 0.78614 
with T in [K] and ew in [hPa] 
4: Hyland and Wexler, 1983 Log ew =  -0.58002206 104 / T
                 + 0.13914993 101 
                 - 0.48640239 10-1 T 
                 + 0.41764768 10-4 T2 
                 - 0.14452093 10-7 T3 
                 + 0.65459673 101 Log(T) 
with T in [K] and ew in [Pa]
5: Hardy, 1998 Log ew =  -2.8365744 103 / T2
                 - 6.028076559 103 / T
                 + 1.954263612 101
                 - 2.737830188 10-2 T
                 + 1.6261698 10-5 T2 
                 + 7.0229056 10-10 T3 
                 + 1.8680009 10-13 T4 
                 + 2.7150305 Log(T)
with T in [K] and ew in [Pa]
6: Buck, 1996
Updated equation from Buck (1981)

ew = 6.1121  e(18.678 - t / 234.5) t / (257.14 + t)

with t in [°C] and ew in [hPa]
7: Buck, 1981

ew = 6.1121  e17.502 t / (240.97 + t)      

with t in [°C] and ew in [hPa]
8: Sonntag, 1994 Log ew =  -6096.9385 / T
                 + 16.635794 
                 - 2.711193 10-2 * T 
                 + 1.673952 10-5 * T2 
                 + 2.433502 * Log(T) 
with T in [K] and ew in [hPa]
9: Magnus Tetens
Murray, 1967		 ew = 6.1078 e17.269388 * (T-273.16) / (T – 35.86)
with T in [K] and ew in [hPa]
10: Bolton, 1980 ew = 6.112 e17.67 * t / (t+243.5)
with t in [°C] and ew in [hPa]
11: Murphy and Koop, 2005

Log ew = 54.842763 
                - 6763.22 / T 
                - 4.21 Log(T) 
                + 0.000367 T 
                + Tanh{0.0415 (T - 218.8)} 
                ·  (53.878 - 1331.22 / T - 9.44523 Log(T) + 0.014025 T)

with T in [K] and ew in [Pa]
12: International Association for the Properties of Water and Steam (IAPWS) Formulation 1995
Wagner and Pruß, 2002

Log (ew/22.064e6) = 647.096/T * ((-7.85951783 ν 
                                                            + 1.84408259 ν1.5 
                                                            - 11.7866497 ν3 
                                                            + 22.6807411 ν3.5 
                                                            - 15.9618719 ν4 
                                                            + 1.80122502 ν7.5))

with T in [K] and ew in [Pa] and ν = 1 - T/647.096

Notes: 

  • At low temperatures most of the equations are based on theoretical studies and only a small number are based on actual measurements of the vapor pressure. The equation by Goff and Gratch [1] for the vapor pressure over liquid water covers a region of -50°C to 102°C [Gibbins 1990]. This work has generally been considered the reference equation but other equations are in use in the meteorological community [Elliott and Gaffen, 1993]. There is a very limited number of measurements of the vapor pressure of water over supercooled liquid water at temperatures below °C. Detwiler [1983] claims some indirect evidence to support the extrapolation of the Goff-Gratch equation down to temperatures of -60°C. However, this remains an open issue.
  • The WMO Guide to Meteorological Instruments and Methods of Observation (CIMO Guide, WMO No. 8) formulation [2] is widely used in Meteorology and appeals for its simplicity. Together with the formulas by Bolton [9] and Buck [7] it has the same mathematical form as older the Maguns Tetens [9] formula and differs only in the value of the parameters.
  • The equation by Hardy [5] is used by Vaisala and is very similar to the formula by Sonntag [8]. This formula is equivalent to the older formula by Wexler (1976), with coefficients that were update to the ITS-90 temperature scale. The differences between Hardy (1998), Hyland and Wexler (1983) and Wexler (1976) are small.
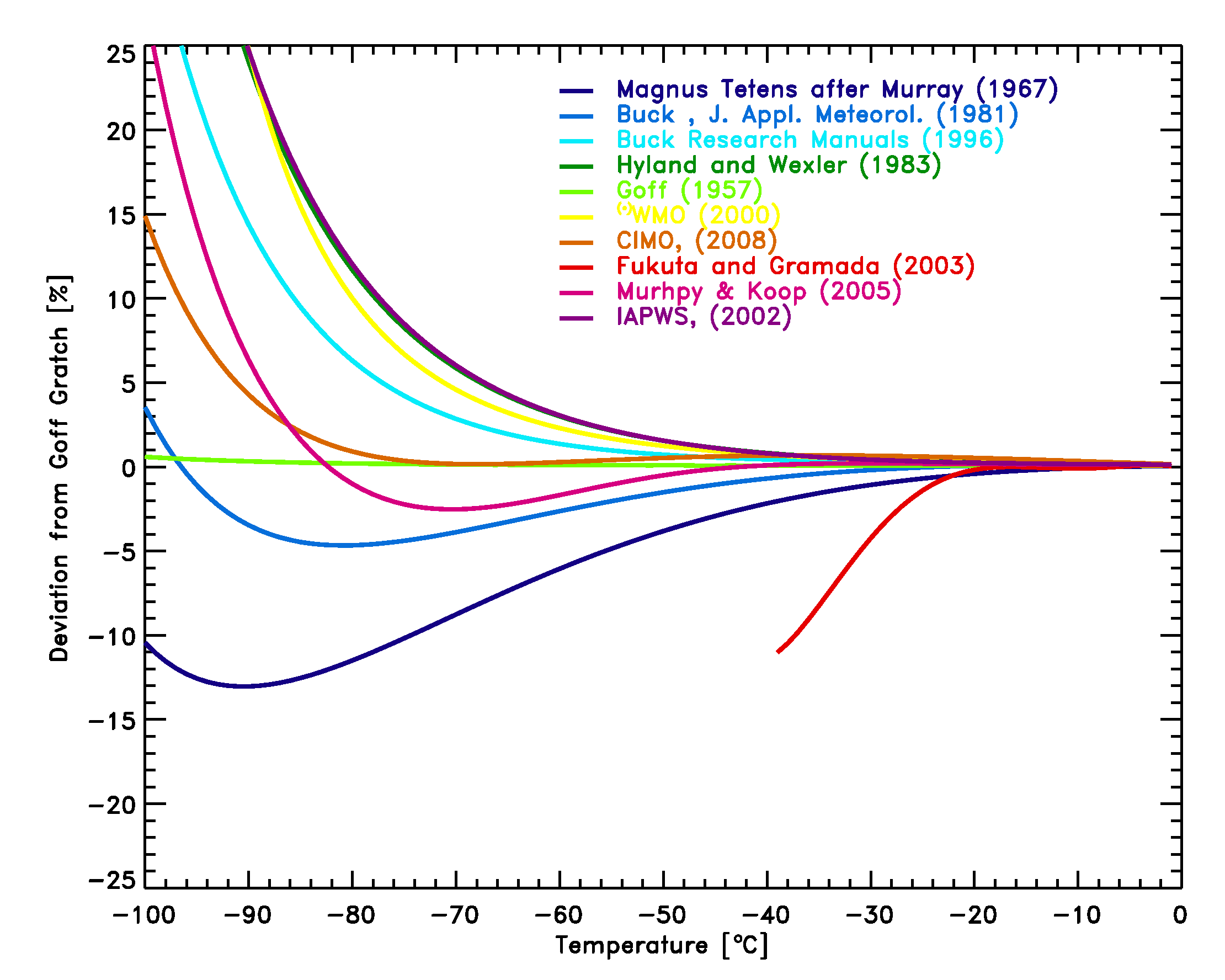
  • The comparison for the liquid saturation vapor pressure equations [2]-[12] with the Goff-Gratch equation [1] in Figure 1 shows that uncertainties at low temperatures become increasingly large and reach the measurement uncertainty claimed by some RH sensors. At -60°C the deviations range from -6% to +3% and at -70°C the deviations range from -9% to +6%. For RH values reported in the low and mid troposphere the influence of the saturation vapor pressure formula used is small and only significant for climatological studies [Elliott and Gaffen 1993].  
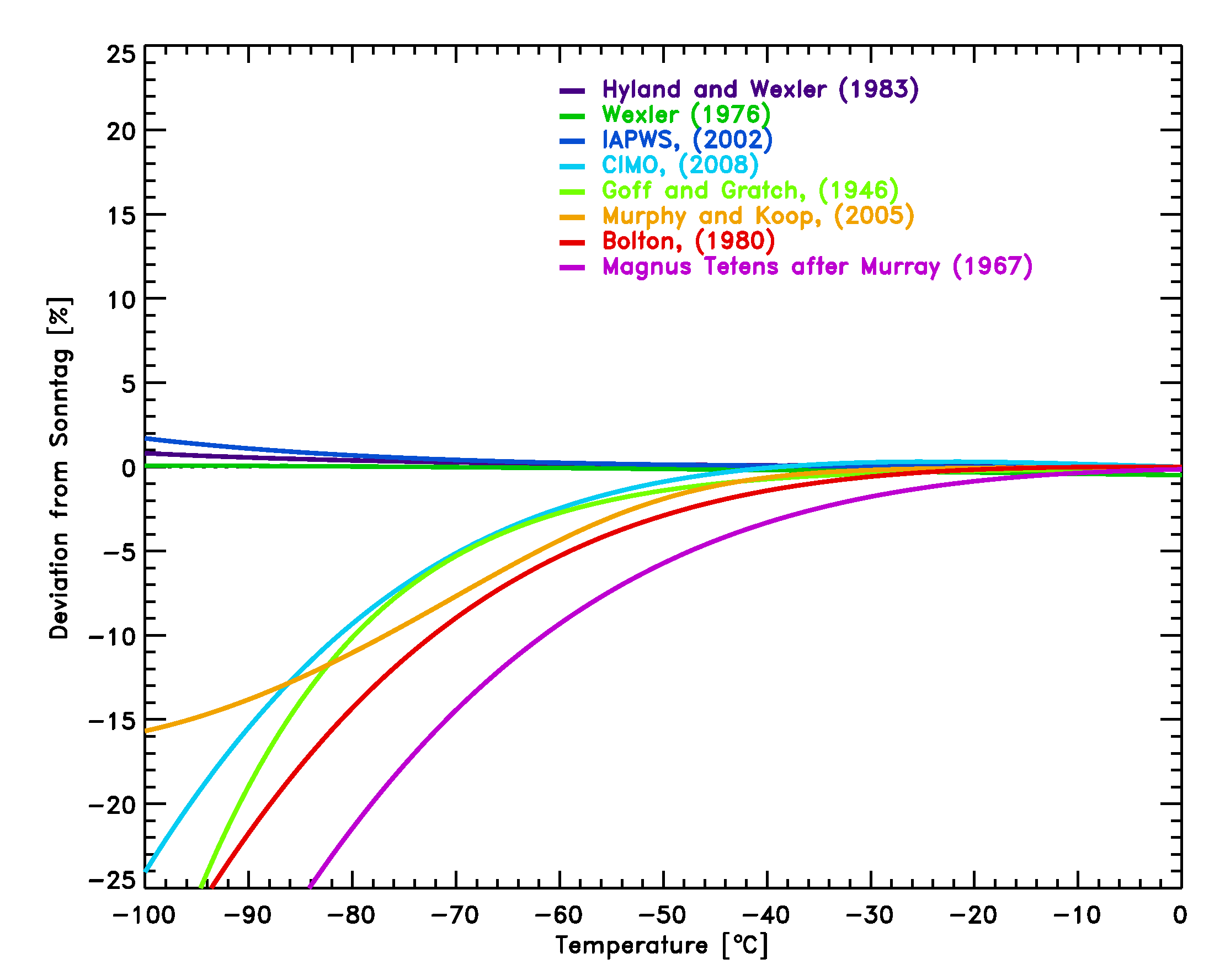
  • The review of vapor pressures of ice and supercooled water by Murphy and Kopp (2005) provides a formulation [11] based on recent data on the molar heat capacity of supercooled water. The comparison of the the vapor pressure equations with the formulation by Murphy and Koop is shown in Figure 2.
  • The study by Fukuta and Gramada [2003] shows direct measurements of the vapor pressure over liquid water down to -38°C. Their result indicates that at the lowest temperatures the measured vapor pressure may be as much as 10% lower than the value given by the Smithsonian Tables [1], and as shown in Figure 1 lower as any other vapor pressure formulation. However, these data are in conflict with measured molar heat capacity data (Muprhy and Koop, 2005), which have been measured both for bulk as for small water droplets.
  • Like most other formulations, the IAPWS formulation 1995 (Wagner and Pruß, 2002) are valid only above the triple point, i.e. in the temperature range 273.16 K < T < 647.096 K.
  • It is important to note that in the upper troposphere, water vapor measurements reported in the WMO convention as relative humidity with respect to liquid water depend critically on the saturation vapor pressure equation that was used to calculate the RH value.

Vapor Pressure Liquid

Figure 1: Comparison of equations [2]-[11] with the Goff Gratch equation [1] for the saturation pressure of water vapor over liquid water. The measurements by Fukuta et al. [2003] are shown as well.

Vapor Pressure Liquid SO

Figure 2: Comparison of several equations with the equation by Sonntag [7] for the saturation pressure of water vapor over liquid water.


The equations by Hyland and Wexler [4], the nearly identical equation by Wexler (1976, see reference below) and the equation by Sonntag [7] are the most commonly used equations among radiosonde manufacturers and should be used in upper air applications to avoid inconsistencies.

 

 

2. Vapor pressure over ice

13: Goff Gratch equation
Smithsonian Tables, 1984		 Log10 ei =  -9.09718 (273.16/T - 1)
                   - 3.56654 Log10(273.16/ T) 
                   + 0.876793 (1 - T/ 273.16) 
                   + Log10(6.1071) 
with T in [K] and ei in [hPa]
14: Hyland and Wexler, 1983 Log ei =  -0.56745359 104 / T
               + 0.63925247 101 
               - 0.96778430 10-2 T 
               + 0.62215701 10-6 T2 
               + 0.20747825 10-8 T3 
               - 0.94840240 10-12 T4 
               + 0.41635019 101 Log(T) 
with T in [K] and ei in [Pa]
15: Guide to Meteorological Instruments and Methods of Observation (CIMO Guide)
WMO, 2008		 ei = 6.112 e(22.46 t/(272.62 + t)) 
with t in [°C] and ei in [hPa]
16: Magnus Teten
Murray, 1967		 ei = 6.1078 e21.8745584 * (T-273.16) / (T – 7.66) 
with T in [K] and ew in [hPa]
17: Buck, 1996
Updated equation from Buck (1981)

ei = 6.1115  e(23.036 - t / 333.7) t / (279.82 + t)

with t in [°C] and ei in [hPa]
18: Buck, 1981

ei = 6.1115 e22.452 t / (272.55+t)

with t in [°C] and ei in [hPa]
19: Marti and Mauersberger, 1993 Log10 ei = -2663.5 / T + 12.537
with T in [K] and ei in [Pa]
20: Murphy and Koop, 2005 Log ei = 9.550426 
              - 5723.265/T 
              + 3.53068 Log(T) 
              - 0.00728332 T
with T in [K] and ei in [Pa]
21: Sonntag, 1994 Log ei =  -6024.5282 / T
               + 24.7219 
               + 1.0613868 10-2 * T 
               + 1.3198825 10-5 * T2 
               - 0.49382577 * Log(T) 
with T in [K] and ew in [hPa]

Notes:

  • The Goff Gratch equation [11] for the vapor pressure over ice covers a region of -100°C to 0°C. It is generally considered the reference equation; however, other equations have also been widely used. The equations discussed here are mostly of interest for frost-point measurements using chilled mirror hygrometers, since these instruments directly measure the temperature at which a frost layer and the overlying vapor are in equilibrium. In meteorological practice, relative humidity is given over liquid water (see section 1) and care needs to be taken to consider this difference.
  • Buck Research, which manufactures frost-point hygrometers, uses the Buck formulations in their instruments. These formulations include an enhancement factor, which corrects for the differences between pure vapor and moist air. This enhancement factor is a weak function of temperature and pressure and corrects about 0.5% at sea level. For the current discussion it has been omitted.
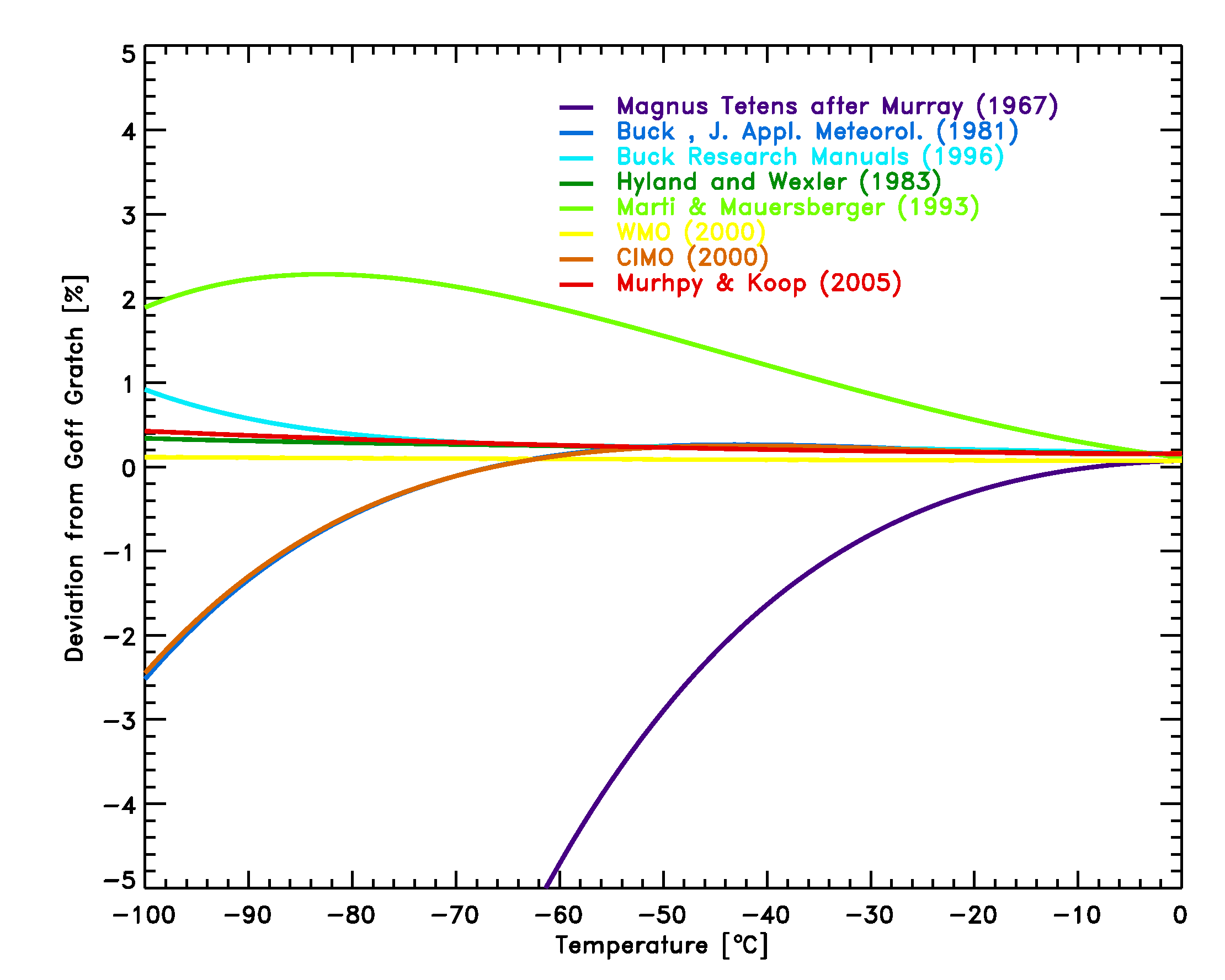
  • The Marti Mauersberger equation is the only equation based on direct measurements of the vapor pressure down to temperatures of 170 K. The comparison of equations 12-17 with the Goff Gratch equation (figure 3) shows, that with the exception of the Magnus Teten formula, the deviations in the typical meteorological range of -100°C to 0°C are less than 2.5%, and smaller than typical instrumental errors of frost-point hygrometers of 5-10%.
  • Not shown is the WMO recommended equation for vapor pressure over ice, since it is nearly identical with the Goff-Gratch equation [12].

 

Vapor Pressure

Figure 3: Comparison of equations [14]-[19] with the Goff Gratch equation [13] for the saturation pressure of water vapor over ice.

 

3. References

  • Bolton, D., The computation of equivalent potential temperature, Monthly Weather Review, 108, 1046-1053, 1980..
  • Buck, A. L., New equations for computing vapor pressure and enhancement factor, J. Appl. Meteorol., 20, 1527-1532, 1981.
  • Buck Research Manuals, 1996
  • Detwiler, A., Extrapolation of the Goff-Gratch formula for vapor pressure over liquid water at temperatures below 0°C, J. Appl. Meteorol., 22, 503, 1983.
  • Elliott, W. P. and D. J. Gaffen, On the utility of radiosonde humidity archives for climate studies, Bull. Am. Meteorol. Soc., 72, 1507-1520, 1991.
  • Elliott, W. P. and D. J. Gaffen, Effects of conversion algorithms on reported upper air dewpoint depressions, Bull. Am. Meteorol. Soc., 74, 1323-1325, 1993.
  • Fukuta, N. and C. M. Gramada, Vapor pressure measurement of supercooled water, J. Atmos. Sci., 60, 1871-1875, 2003.
  • Gibbins, C. J., A survey and comparison of relationships for the determination of the saturation vapour pressure over plane surfaces of pure water and of pure ice, Annales Geophys., 8, 859-886, 1990.
  • Goff, J. A., and S. Gratch, Low-pressure properties of water from -160 to 212 F, in Transactions of the American society of heating and ventilating engineers, pp 95-122, presented at the 52nd annual meeting of the American society of heating and ventilating engineers, New York, 1946.
  • Goff, J. A. Saturation pressure of water on the new Kelvin temperature scale, Transactions of the American society of heating and ventilating engineers, pp 347-354, presented at the semi-annual meeting of the American society of heating and ventilating engineers, Murray Bay, Que. Canada, 1957.
  • Hardy, B., 1998, ITS-90 Formulations for Vapor Pressure, Frostpoint Temperature, Dewpoint Temperature, and Enhancement Factors in the Range –100 to +100 °C, The Proceedings of the Third International Symposium on Humidity & Moisture, London, England
  • Hyland, R. W. and A. Wexler, Formulations for the Thermodynamic Properties of the saturated Phases of H2O from 173.15K to 473.15K, ASHRAE Trans, 89(2A), 500-519, 1983.
  • Marti, J. and K Mauersberger, A survey and new measurements of ice vapor pressure at temperatures between 170 and 250 K, GRL 20, 363-366, 1993
  • Murphy, D. M. and T. Koop, Review of the vapour pressures of ice and supercooled water for atmospheric applications, Quart. J. Royal Met. Soc, 131, 1539-1565, 2005.
  • Murray, F. W., On the computation of saturation vapor pressure, J. Appl. Meteorol., 6, 203-204, 1967.
  • Smithsonian Met. Tables,  5th ed., pp. 350, 1984.
  • Sonntag, D., Advancements in the field of hygrometry, Meteorol. Z., N. F., 3, 51-66, 1994.
  • Wagner W. and A. Pruß, The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use, J. Phys. Chem. Ref. Data, 31, 387-535, 2002.
  • Wexler, A., Vapor Pressure Formulation for Water in Range 0 to 100°C. A Revision, Journal of Research of the National Bureau of Standards, 80A, 775-785, 1976.
  • World Meteorological Organization, Technical Regulations, Basic Documents No. 2, Volume I - General meteorological standards and recommended practices, Appendix A, WMO-No. 49, Geneva 2011, updated 2012.
  • World Meteorological Organization, Guide to Meteorological Instruments and Methods of Observation, Appendix 4B, WMO-No. 8 (CIMO Guide), Geneva 2008.
IDL Source for all equations

 

Contact 

voemel@ucar.edu 

 

Page Updated 2/10/2025